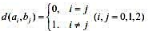题目内容
(请给出正确答案)
题目内容
(请给出正确答案)
如果一个离散信源的失真矩阵按行划分成若千个子集,并且每行的元素是其他行元素的置换,解列的元
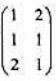 ,可以按行分为两个对称子矩阵:
,可以按行分为两个对称子矩阵: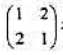 和(1 1),所以此矩阵是行准对称失真矩阵。
和(1 1),所以此矩阵是行准对称失真矩阵。(1)证明如果离散信源的失真矩阵足行准对称失真矩阵,且在划分的子矩阵中信源输入符号的概半相等,那么通过与失真地阵具有同样对称性且满足失真约束的试验信道可以达到R(D)。
(2)一个包含3符号的信源X。符号集为{-1,0,1},概率分别为: p,1-2p,P, (p≤1/2):试验信道输出Y,符号集含2个符号{-1,1},失真测度为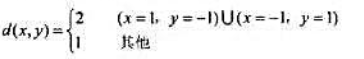 求R(D)函数。
求R(D)函数。
 如果结果不匹配,请 联系老师 获取答案
如果结果不匹配,请 联系老师 获取答案


 更多“如果一个离散信源的失真矩阵按行划分成若千个子集,并且每行的元…”相关的问题
更多“如果一个离散信源的失真矩阵按行划分成若千个子集,并且每行的元…”相关的问题
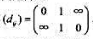 , 可以按列分解为两个对称子矩阵:
, 可以按列分解为两个对称子矩阵: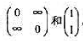 所以此失真矩阵为按列划分的准对称失真矩阵。
所以此失真矩阵为按列划分的准对称失真矩阵。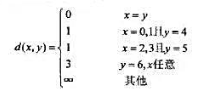 证明,R(D)函数如图9.1所示。
证明,R(D)函数如图9.1所示。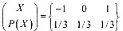 时.按收符号
时.按收符号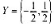 其失真矩阵为
其失真矩阵为 。 求信源的最大平均失真度和最小平均失真度,并求选择何种信道可达到该Dmax和Dmin的失真度。
。 求信源的最大平均失真度和最小平均失真度,并求选择何种信道可达到该Dmax和Dmin的失真度。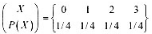 接收符号Y={0,1,2.3}, 其失真矩阵为
接收符号Y={0,1,2.3}, 其失真矩阵为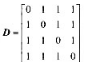 。求Dmax和Dmin以及信源的R(D)函数,并画出R(D)的曲线(取4至5个点)。
。求Dmax和Dmin以及信源的R(D)函数,并画出R(D)的曲线(取4至5个点)。 其中,p<1/2.求信源的R(D)函数,并画出曲线。
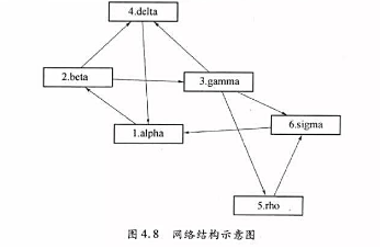
其中,p<1/2.求信源的R(D)函数,并画出曲线。 它们分别给出了页面j的链人链接数目和页面i的链出链接数目。假如在上网时浏览页面并选择下一个页面的过程,与过去浏览过哪些页面无关,而仅依赖于当前所在的页面。那么这一-选择过程可以认为是一一个有限状态、离散时间的随机过程,其状态转移规律用Markov链描述。定义矩阵A=(ay)wxn为
它们分别给出了页面j的链人链接数目和页面i的链出链接数目。假如在上网时浏览页面并选择下一个页面的过程,与过去浏览过哪些页面无关,而仅依赖于当前所在的页面。那么这一-选择过程可以认为是一一个有限状态、离散时间的随机过程,其状态转移规律用Markov链描述。定义矩阵A=(ay)wxn为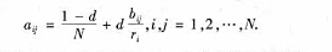 式中:d是模型参数,通常取d=0.85;A是Markov链的转移概率矩阵;ay表示从页面i转移到页而j的概率。根据Markov链的基本性质,对于正则Markov链存在平稳分布x=
式中:d是模型参数,通常取d=0.85;A是Markov链的转移概率矩阵;ay表示从页面i转移到页而j的概率。根据Markov链的基本性质,对于正则Markov链存在平稳分布x= 式中:x为在极限状态(转移次数趋于无限)下各网页被访问的概率分布,Google将它定义为各网页的PageRank值。假设x已经得到,则它按分量满足方程
式中:x为在极限状态(转移次数趋于无限)下各网页被访问的概率分布,Google将它定义为各网页的PageRank值。假设x已经得到,则它按分量满足方程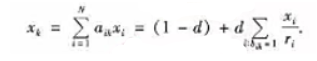 网页i的PageRank值是划,它链出的页面有τ个,于是页面i将它的PageRank值分成r份,分别“投票"给它链出的网页。x为网页k的PageRank值,即网络上所有页面“投票给网页k的最终值。根据Markov链的基本性质还可以得到,平稳分布(即PageRank值)是转移概率矩阵A的转置矩阵AT的最大特征值(=1)所对应的归一化特征向量。
网页i的PageRank值是划,它链出的页面有τ个,于是页面i将它的PageRank值分成r份,分别“投票"给它链出的网页。x为网页k的PageRank值,即网络上所有页面“投票给网页k的最终值。根据Markov链的基本性质还可以得到,平稳分布(即PageRank值)是转移概率矩阵A的转置矩阵AT的最大特征值(=1)所对应的归一化特征向量。