题目内容
（请给出正确答案）
[单选题]
在模型 中, x1 符合形状参数为 3.5和特征寿命为 20的威布尔分 布， x2符合对数为 16并且标准差（σ)为 2.5的对数分布，并且 是个平均数为 0且σ为1的随机变 量。在这种情形下，下列哪种方法是最佳评估 y的分布？
A.回归分析
B.蒙特卡罗仿真
C.方差分析法
D.数值积分
查看答案
如果结果不匹配，请 联系老师 获取答案
题目内容
（请给出正确答案）
如果结果不匹配，请 联系老师 获取答案
题目内容
（请给出正确答案）
A.回归分析
B.蒙特卡罗仿真
C.方差分析法
D.数值积分
如果结果不匹配，请 联系老师 获取答案
更多“ 在模型 中, x1 符合形状参数为 3.5和特征寿命为 2…”相关的问题
某商品的需求函数为：
lnYi=92.3+0.46lnX1t-0.18lnX2t
(0.126) (0.032)
(3.651) (-5.625)
R^2=0.983,调整后的R^2=0.976，F=581
其中，Y为需求量，X1为消费者收入，X2为该商品价格。
(1)解释参数的经济意义;(2)若价格上涨10%将导致需求如何变化？
(3)在价格上涨10%的情况下，收入增加多少才能保持需求不变？(4)解释模型中各个统计量的含义。
在3.4节消费者的选择模型中，
(I)证明若条件(3)成立,则u(x1,x2)=e是单调减、下凸的曲线，
(2)验证(4),(6),(8)式给出的效用两数是否满足条件(3)，
(3)若消费者的效用函数为(8)式,求最优比例p1q1/p2q2,并分析参数a,b的意义。
(4)若商品甲的价格P,增加,其余条件不变,讨论消费点Q的变化。
(5)若消费者购买商品的钱s增加,其余条件不变,讨论消费点Q的变化。
(6)推广到消费者购买m(>2)种商品的情况。
考虑含有三个自变量的多元回归模型,并满足假定MLR.1到MLR.4,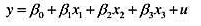
你对估计x1和x2,的参数之和感兴趣;把这个和记为θ1=β1+β2.
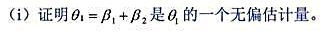
A.异方差
B.完全多重共线
C.遗漏变量偏差
D.虚拟变量陷阱
设总体X的概率密度为.
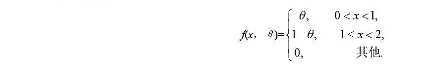其中9是未知参数(0＜ 0＜1)X1,X2…Xn为来自总体X的简单随机样本，记N为样本值X1,X2…Xn中小于1的个数，求:
(1)
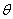的矩估计:
(2)
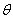的最大似然估计.
2
(σ≠0)。证明：当n充分大时，算术平均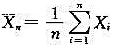
近似服从正态分布，并指出分布中的参数。
A.当X2不变时，X1每变动一个单位Y的平均变动
B.当X1不变时，X2每变动一个单位Y的平均变动
C.当X1和X2都保持不变时，Y的平均变动
D.当X1和X2都变动一个单位时，Y的平均变动
